PVT는 제목처럼, 압력-부피-온도의 상관관계를 나타낸 것이다. 압력, 온도에 따라 재료의 상(Phase)이 바뀌고, 이에 따라 부피(체적)가 변하는 특징을 말한다. 고분자뿐만 아니라, 다른 재료에서도 이러한 관계가 나타난다.
아래는 대표적인 물에 대한 PVT 그래프다. 1 기압 기준 0도씨를 기점으로 고체와 액체로 나뉘고 100도가 넘어가면 증발한다. 압력이 좀 더 높다면, 0도보다 낮은 온도에서 액체가 되기도 한다. 저기서 보이는 'Critical point'는 초임계점으로서, 액체와 기체를 구분할 수 없는 시점을 말한다. 초임계 상태에서 분자의 밀도는 액체와 비슷하지만, 점성도는 매우 낮아 기체와 가까운 상태다.
고분자에선 PVT 관계가 왜 필요할까? 일단 고분자란 단량체 분자들의 화학반응을 통하여 규칙적인 반복 단위를 가진 긴 사슬로 이루어진 분자이다. 분자 사슬은 segment라고 보면 되며 즉, 분자량이 아주 많고 큰 분자를 고분자라고 한다.
그리고 고분자를 인종적으로 합성해서 만든 것이 합성수지이며. 합성수지는 '열가소성 수지(열을 받아 녹아버리면 체적이 늘어나고, 다시 냉각되면 체적이 줄어든다.)'와 '열경화성 수지(열을 가하면 녹지 않고, 타서 가루가 되거나 기체가 된다. 한번 굳어지면 다시 녹지 않는다.)'로 나뉜다.
즉, 열가소성 수지를 다룰 때 PVT 관계가 해당이 된다. 보통 열가소성 수지를 이용해 만드는 제품들은 대부분 작은 고체들을 넣어서 녹인 다음, 원하는 모양을 만들어서 굳게 한다. 고상 -> 액상 -> 고상으로 가기 때문에 이때 제품에 부피가 얼마나 달라질지, 너무 수축해서 문제가 생기지는 않을지를 확인하기 위해 PVT 관계를 이용하는 것이다.
- 2020.12.28 - [과학과 공학 이야기/고분자] - PVT ; Pressure, Volume, Temperature 거동이란?
- 2021.07.13 - [과학과 공학 이야기/고분자] - 고분자 결정화 구조, 결정성과 비결정성, 아브라미와 나카무라 방정식
아래는 고분자의 PVT 곡선의 예시이다. p0은 일반 대기압 상태를 나타내는 것이고, p1은 증가한 압력이다. b5는 상이 변하는 상전이 온도이며 결정화 온도라고도 얘기한다.
곡선을 보면, b6의 위치가 압력이 커질수록 x축에서 오른쪽으로 가는 것을 볼 수 있다. 이는 압력이 커질수록 상전이 온도가 증가한다는 것을 의미한다. 참고로 b6은 압력에 따라 변하는 상전이 온도를 설명하기 위한 매개변수 값이다.
왼쪽과 오른쪽 그래프의 모양이 다소 다른 점을 볼 수 있는데, 왼쪽은 쓰여있듯이 비정질 재료이고, 오른쪽은 반결정 재료이다. 이전에 고분자의 비결정성(=비정질)과 결정성(=반결정성) 수지에 대하 얘기를 한 적이 있는데, 그와 통하는 얘기다.
비정질 재료는 비결정형 구조만 있기 때문에 유리전이온도만 존재하므로 온도가 올라갈수록 부피가 부드러운 모양으로 증가한다. 하지만 반결정성 재료는 비결정형 구조가 먼저 녹으면서 서서히 부피가 증가하다가, 대부분의 구조를 형성하고 있는 결정성 구조가 녹기 시작하면서 급격하게 부피가 증가한다.
저렇듯 반결정성 재료에서는 고상과 액상에서의 부피 변화가 급격히 일어나기 때문에 부피 차이가 크고, 곡선도 위와 같이 큰 차이를 보인다.
이 때문에 기존에 PVT 곡선을 설명하는 Tait 모델은 기준 온도가 상전이 온도 이하 거나, 클 때는 고려하여 각각 다른 수식을 수정 및 적용했다. 이를 '2-domain Tait EOS' 모델이라고 하며, 수정된 Tait 모델이라고도 부른다. 또한, 온도와 압력 두 가지 변수를 고려하는 만큼, 측정하는 장비도 그렇게 많지 않고 PVT 측정 비용도 굉장히 비싼 듯하다.
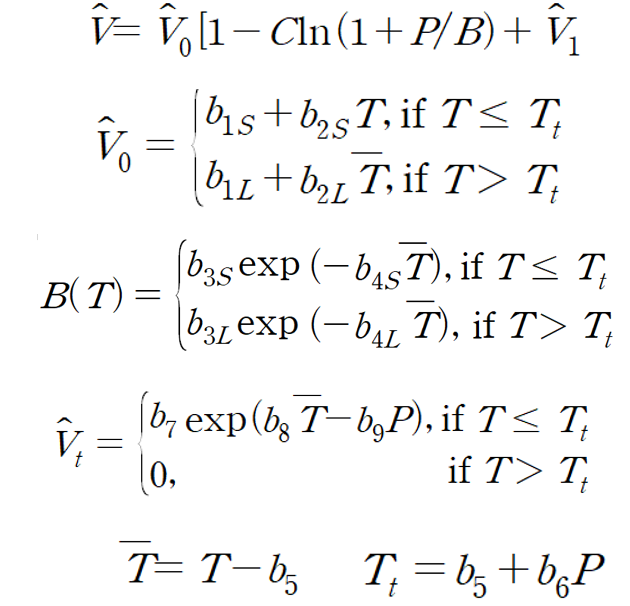
'과학과 공학 이야기 > 고분자' 카테고리의 다른 글
| 고분자의 고체 점탄성 : Generalized Maxwell model, 일반화된 맥스웰 모델 (0) | 2021.09.03 |
|---|---|
| 고분자의 유리전이온도, 결정화온도, 용융온도 정의와 차이 Tg, Tc, Tm 차이 (11) | 2021.08.18 |
| 고분자 결정화 구조, 결정성과 비결정성, 아브라미와 나카무라 방정식 (2) | 2021.07.13 |
| 뉴턴 유체와 비뉴턴 유체 정리, Newtonian fluid, Non-Newtonian fluid (0) | 2021.07.03 |
| 아레니우스 식에 대한 요약 및 정리, 아레니우스 점도 (6) | 2021.06.27 |
댓글