고분자를 포함한 유체(엑체와 기체를 통틀어 말함)에서 항상 적용되는 것이 유체역학이다. 유체역학은 유체 흐름에 대한 압력, 속도, 고도 사이 관계를 설명한다.
유체역학 중 하나로 1738년 다니엘 베르누이가 방정식을 고안하는데, 이게 '베르누이 방정식'이다.
베르누이 방정식이 적용되는 대표적인 예로는 컨테이너나 배관에서 액체가 얼마나 빨리 배출이 될 수 있는지나, 비행기가 앙력으로 인해 위로 뜨는 이유를 설명할 수 있다. *물론 비행기는 유체역학 외 다양한 이유가 있겠지만 말이다.
'Bernoulli equation(베르누이 방정식)'
간단하게 말하면 베르누이 방정식은 '정압력과 동압력의 합은 언제나 같다'로 설명할 수 있으며, 유체역학에서 적용되는 에너지 보존 법칙이라고 보면 된다. 다만, 압력에 따라 유체의 밀도가 변하지 않은 '비압축성 유체'라고 가정해야 한다.
*'정압(static pressure)'은 우리가 흔히 생각하는 압력, '동압(dynamic pressure)'은 유체의 운동을 막았을 때 생기는 압력을 말한다. 이 두 개를 합하면 '전압(total pressure)'라고 한다.
높이에 따른 압력
처음부터 조금씩 살펴보자. '밀도'는 '질량/부피'이다. 그리고 '무게'는 '질량*중력가속도'이다. 이걸 적용하면 유체의 무게는 '밀도 * 부피 * 중력가속도'로 표현이 가능하며, 부피는 단면적 * 높이다.
*참고로 질량은 중력과 상관없이 물질이 기본적으로 가진 속성이며, 무게는 물체가 중력에 의해 받는 힘(force)을 의미한다. 질량에 비례한다.
정리하면 위치에 따른 압력(P)은 pgh로 표현이 가능하다. 즉, 이는 위치가 높을수록 압력이 높아지고, 낮아지면 압력도 낮아짐을 의미한다. 다만, 이 역시 '비압축성 유체'임을 가정한다.

높이와 압력이 비례함을 알게 됐으면, 다음식을 살펴보자. P0는 대기압을 의미하며, P'는 물체가 실제로 받는 압력을 의미한다. 이 두 압력을 합치면 유체가 실제로 적용받는 압력을 의미한다.
F(힘)은 유체가 받는 압력과 단면적을 곱하여 얻을 수 있다. 이를 적용했을 때 위치에 따라 적용받는 힘이 다르며, 이 힘에 차이가 '부력'이 된다.


'정상류(steady flow)'란?
'정상류'란 유체의 흐름이 시간에 따라 변하지 않은 것을 의미한다. 아래와 같은 사진에서 왼쪽이 정상류, 오른쪽은 비정상류(unsteady flow)를 의미한다.
정상류는 유체의 흐름이 변하지 않기 때문에 위치에 따른 질량도 동일하다. 아래 사진에서 왼쪽 하단에 있는 위치에서의 질량이나, 오른쪽 위에 있는 유체의 질량이나 흐름이 변하지 않기 때문에 동일하다.

아래 사진을 보자. 유체가 정상류임을 가정할 때, 질량은 밀도 * 부피로 나타낼 수 있고, 델타 t는 시간이다. 즉, 시간에 따라 흐르는 질량의 양을 구할 수가 있다. 그런데 정상류임을 가정하면, 시간에 따른 유체의 흐름을 변함이 없기 때문에 질량도 동일하다.
즉, 아래 오른쪽 식을 이용해 소거하면, 단면적이 크면 속도가 낮아지고, 단면적이 낮으면 속도가 올라감을 알 수가 있다. 우리가 호스에서 앞쪽을 손으로 누르면 물이 더 빠른 속도로 배출되는데 바로 이러한 이유 때문이다.


이를 이해하고 넘어가면, 이제 '베르누이 방정식(Bernoulli equation)'을 살펴보자.
· 베르누이 방정식은 위에 있는 모든 설명을 한 번에 압축시킨 방정식이다.
· 한마디로 유체의 속력에 따라 압력이 변화하며, 속력, 압력, 높이 관계를 설명한 식이다. 베르누이 방정식은 하단과 같은 식으로 나타낼 수 있다.
· 여기서 P는 앞서 언급한 우리가 흔히 생각하는 압력인 정압. 우리가 가하게 될 압력이다. pv^2/2는 유체가 힘에 의해 멈췄을 때 발생하는 압력인 동압으로 나뉜다. 여기에 pgh를 합하는 것은 위치에 따른 압력을 고려하기 때문인데, 실제 유선(streamline)에 적용할 땐 영향력이 적어 무시하는 경우도 있다.
· 그리고 이 정압과 동압, 위치에 따른 압력을 합치면 전압(total pressure)이 되고, 베르누이 방정식에서 전압은 언제나 동일하다는 것을 의미한다. 또한, 정압과 동압의 합은 일정하기 때문에 유관이 넓을 땐 속도가 작고, 압력이 크다. 반대로 유관이 좁을 땐 속도가 크고 압력이 작아짐을 설명할 수 있다.
· 예를 들어 비행기의 날개 위쪽은 더 휘어져있는 반면, 아래쪽은 플랫하다. 이는 비행기 위쪽으로 흐르는 공기의 흐름이 빨라 압력이 낮고 아래 평평한 쪽은 흐름이 느려 속도가 낮아 압력이 높다. 이 두 압력의 차이로 양압이 발생하고, 비행기가 위로 뜨게 된다.
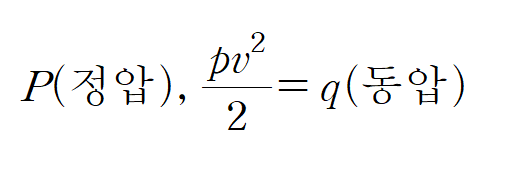
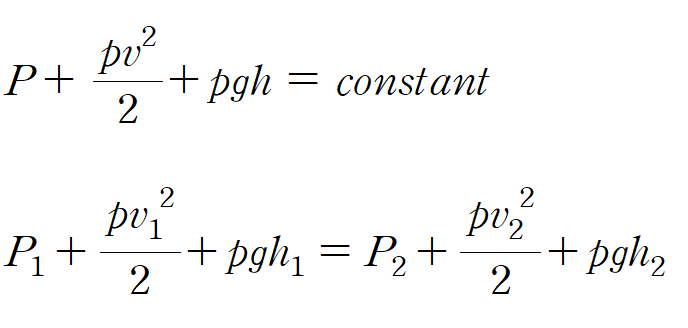
토리첼리의 정리(Torricelli's theorem)
· 토리첼리의 정리는 베르누이 방정식에서 유도된 것이며, 구멍을 통해 배출되는 유체의 속도 값을 계산하는 공식이다.
· 하단과 같은 식으로 표현할 수 있고, 이를 이용하면 반대로 유체의 속도를 통해 압력을 구하는 것도 가능하다. *단, 이때 구멍이 작음을 가정해 유체의 하강 속도는 무시한다.
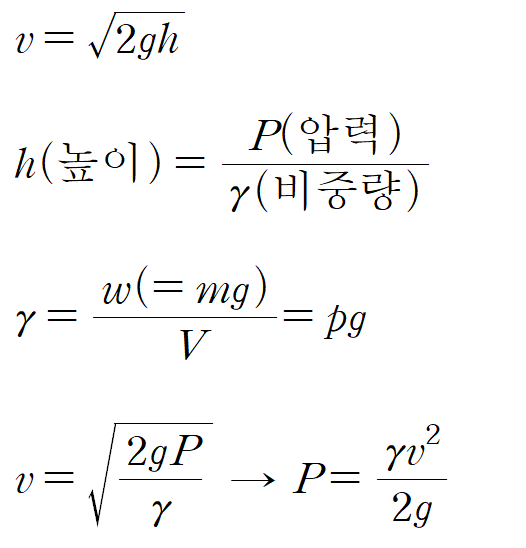




댓글